ĐÁP ÁN ĐỀ THI GIỮA HỌC KÌ I TOÁN 8 TRƯỜNG THPT CHUYÊN HÀ NỘI AMSTERDAM NĂM 2020 - 2021
Ngày đăng: 05/11/2020
Cộng đồng zalo giải đáo bài tập
Các bạn học sinh tham gia nhóm zalo để trao đổi giải đáp bài tập nhé
| Con sinh năm 2009 | https://zalo.me/g/cieyke829 |
| Con sinh năm 2010 | https://zalo.me/g/seyfiw173 |
| Con sinh năm 2011 | https://zalo.me/g/jldjoj592 |
| Con sinh năm 2012 | https://zalo.me/g/ormbwj717 |
| Con sinh năm 2013 | https://zalo.me/g/lxfwgf190 |
| Con sinh năm 2014 | https://zalo.me/g/bmlfsd967 |
| Con sinh năm 2015 | https://zalo.me/g/klszcb046 |
|
TRƯỜNG THPT CHUYÊN HÀ NỘI – AMSTERDAM TỔ TOÁN – TIN
|
ĐÁP ÁN ĐỀ KIỂM TRA GIỮA HỌC KÌ I MÔN: TOÁN LỚP 8 Năm học: 2020 – 2021 Thời gian làm bài: 60 phút |
Bài 1. (3,0 điểm)
Phân tích các đa thức sau thành nhân tử:
1) $A\left( x \right)={{x}^{2}}-3x+2$ 2) $B\left( x;y \right)={{x}^{2}}+4{{y}^{2}}-4xy-4$
Bài 2. (2,0 điểm)
Tìm x sao cho ${{\left( x-2 \right)}^{3}}+{{\left( 2x+1 \right)}^{3}}-9{{\left( x+1 \right)}^{3}}=-16$
Bài 3. (1,0 điểm)
Cho a, b, c là các số thực thỏa mãn ${{a}^{2}}+{{b}^{2}}+{{c}^{2}}=ab+bc+ca$. Chứng minh rằng $a=b=c$
Bài 4. (3,5 điểm)
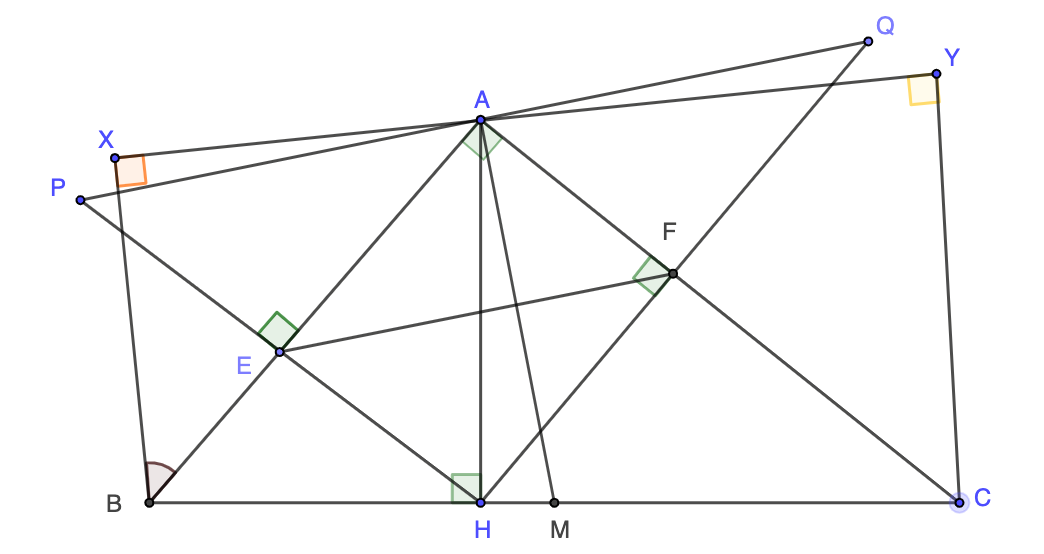
Cho tam giác ABC vuông tại A (AB < AC), đường cao AH, đường trung tuyến AM. Gọi E, F lần lượt là hình chiếu vuông góc của H trên AB, AC. Trên tia đối của EH lấy điểm P sao cho EP = EH, trên tia đối của FH lấy Q sao cho FH = FQ.
- Chứng minh ba điểm P, A, Q thẳng hàng.
- Chứng minh rằng tứ giác BPQC là hình thang vuông và PQ + QC = BC.
- Chứng minh AM vuông góc với EF.
- Gọi (d) là đường thẳng thay đổi, đi qua A, nhưng không cắt cạnh BC của tam giác ABC. Gọi X, Y lần lượt là hình chiếu vuông góc của B, C trên (d). Tìm vị trí của d dể chu vi tứ giác BXYC lớn nhất.
Bài 5. (0,5 điểm)
1) (Dành cho lớp 8B, 8C, 8D, 8E)
Cho a, b, c là các số thực đôi một khác nhau thỏa mãn ${{a}^{3}}+{{b}^{3}}+{{c}^{3}}=3abc$. Tính giá trị của biểu thức $M=\left( a+b \right)\left( b+c \right)\left( c+a \right)+abc$
2) (Dành riêng cho lớp 8A)
Với a, b là các số thực thỏa mãn ${{a}^{3}}+{{b}^{3}}-3ab=-18$. Chứng minh rằng: $-\,9 HẾT Chú ý: Học sinh không được sử dụng máy tính cầm tay ĐÁP ÁN CHI TIẾT Bài 1. (3,0 điểm) Phân tích các đa thức sau thành nhân tử: 1) $A\left( x \right)={{x}^{2}}-3x+2$ 2) $B\left( x;y \right)={{x}^{2}}+4{{y}^{2}}-4xy-4$ Giải 1) $A\left( x \right)={{x}^{2}}-3x+2$ $={{x}^{2}}-2x-x+2$ $=({{x}^{2}}-2x)-(x-2)$ $=x(x-2)-(x-2)$ $=(x-1)(x-2)$ 2) $B\left( x;y \right)={{x}^{2}}+4{{y}^{2}}-4xy-4$ $=\left( {{x}^{2}}-4xy+4{{y}^{2}} \right)-4$ $={{\left( x-2y \right)}^{2}}-{{2}^{2}}$ $=\left( x-2y-2 \right)\left( x-2y+2 \right)$ Bài 2. (2,0 điểm) Tìm x sao cho ${{\left( x-2 \right)}^{3}}+{{\left( 2x+1 \right)}^{3}}-9{{\left( x+1 \right)}^{3}}=-16$ Giải $\Leftrightarrow {{x}^{3}}-6{{x}^{2}}+12x-8+8{{x}^{3}}+12{{x}^{2}}+6x+1-9({{x}^{3}}+3{{x}^{2}}+3x+1)=-16$ $\Leftrightarrow -21{{x}^{2}}-9x=0$ $\Leftrightarrow -3x\left( 7x+3 \right)=0$ $\Leftrightarrow \left[ \begin{align} & -3x=0 \\ & 7x+3=0 \\ \end{align} \right.$ $\Leftrightarrow \left[ \begin{align} & x=0 \\ & x=-\frac{3}{7} \\ \end{align} \right.$ Vậy $x\in \left\{ \frac{-3}{7};0 \right\}$ Bài 3. (1,0 điểm) Cho a, b, c là các số thực thỏa mãn ${{a}^{2}}+{{b}^{2}}+{{c}^{2}}=ab+bc+ca$. Chứng minh rằng $a=b=c$ Giải Ta có: ${{a}^{2}}+{{b}^{2}}+{{c}^{2}}=ab+bc+ca$ $\Leftrightarrow {{a}^{2}}+{{b}^{2}}+{{c}^{2}}-ab-bc-ca=0$ $\Leftrightarrow 2{{a}^{2}}+2{{b}^{2}}+2{{c}^{2}}-2ab-2bc-2ca=0$ $\Leftrightarrow ({{a}^{2}}-2ab+{{b}^{2}})+({{b}^{2}}-2bc+{{c}^{2}})+({{c}^{2}}-2ca+{{a}^{2}})=0$ $\Leftrightarrow {{(a-b)}^{2}}+{{(b-c)}^{2}}+{{(c-a)}^{2}}=0$ Vì ${{(a-b)}^{2}}\ge 0;\,\,{{(b-c)}^{2}}\ge 0;\,\,{{(c-a)}^{2}}\ge 0\,\,\forall a,b,c$ nên $\Leftrightarrow \left\{ \begin{align} & {{(a-b)}^{2}}=0 \\ & {{(b-c)}^{2}}=0 \\ & {{(c-a)}^{2}}=0 \\ \end{align} \right.$$\Leftrightarrow \left\{ \begin{align} & a-b=0 \\ & b-c=0 \\ & c-a=0 \\ \end{align} \right.$$\Leftrightarrow \left\{ a=b=c \right.$ Vậy $a=b=c$ Bài 4. (3,5 điểm) Cho tam giác ABC vuông tại A (AB < AC), đường cao AH, đường trung tuyến AM. Gọi E, F lần lượt là hình chiếu vuông góc của H trên AB, AC. Trên tia đối của EH lấy điểm P sao cho EP = EH, trên tia đối của FH lấy Q sao cho FH = FQ. Giải Xét ∆PEA và ∆HEA: $\left\{ \begin{align} & PE=HE \\ & \widehat{PEA}=\widehat{HEA} \\ & AE\,chung \\ \end{align} \right.=90{}^\circ \Rightarrow $∆PEA = ∆HEA (c – g – c) $\Rightarrow \widehat{PAE}=\widehat{HAE}$(2 góc tương ứng). $\Rightarrow PA=HA$(2 cạnh tương ứng). Tương tự ta suy ra được ∆HAF = ∆QAF (c – g – c) $\Rightarrow \widehat{HAF}=\widehat{QAF}$ (2 góc tương ứng). $\Rightarrow HA=QA$(2 cạnh tương ứng). $\widehat{HAE}+\widehat{HAF}={{90}^{{}^\circ }}$ (do ∆ABC vuông tại A). $\widehat{PAQ}=\widehat{PAE}+\widehat{HAE}+\widehat{HAF}+\widehat{QAF}=2\widehat{HAE}+2\widehat{HAF}=2.\left( \widehat{HAE}+\widehat{HAF} \right)=2.90{}^\circ ={{180}^{{}^\circ }}$ Vậy P, A, Q thẳng hàng. Xét ∆PBA và ∆HBA: $\left\{ \begin{align} & PA=HA\,(cmt) \\ & \widehat{PAB}=\widehat{HAB}\,\left( cmt \right) \\ & AB\,chung \\ \end{align} \right.\Rightarrow $∆PBA = ∆HBA (c – g – c) $\Rightarrow \widehat{BPA}=\widehat{BHA}$(2 góc tương ứng) $\Rightarrow \widehat{BPA}={{90}^{{}^\circ }}$ hay $BP\bot PQ$. Tương tự ta suy ra $\widehat{CQA}={{90}^{{}^\circ }}$ hay $CQ\bot PQ$. $\left\{ \begin{align} & BP\bot PQ \\ & CQ\bot PQ \\ \end{align} \right.$$\Rightarrow BP//CQ$ $\Rightarrow $ BPQC là hình thang. Hình thang BPQC có $\widehat{BPQ}={{90}^{{}^\circ }}$nên BPQC là hình thang vuông. Ta chứng minh được ∆PEB = ∆HEB (c – g – c) suy ra PB = BH. ∆HFC = ∆QFC (c – g – c) suy ra HC = QC. Suy ra PB + QC = BH + HC = BC. Vậy ta có điều phải chứng minh. Xét hình thang BPQC có A là trung điểm của PQ, M là trung điểm của BC nên AM là đường trung bình của hình thang BPQC. $\Rightarrow AM//BP$. Mà $BP\bot PQ$ nên $AM\bot PQ$. $\Delta $HPQ có $\left\{ \begin{align} & PE=EH \\ & HF=FQ \\ \end{align} \right.\Rightarrow EF$là đường trung bình $\Delta $HPQ $\Rightarrow EF//PQ$ Ta có $\left\{ \begin{align} & AM\bot PQ \\ & PQ//EF \\ \end{align} \right.\Rightarrow AM\bot EF.$ Vậy ta có điều phải chứng minh. Áp dụng bất đẳng thức Bunhiacopxki ta có:${{\left( BX+XA \right)}^{2}}={{\left( BX.1+XA.1 \right)}^{2}}\le (B{{X}^{2}}+X{{A}^{2}}).2$ Mà theo định lý Pi-ta-go trong tam giác ABX vuông tại X : $B{{X}^{2}}+X{{A}^{2}}=A{{B}^{2}}$ $\Rightarrow {{\left( BX+XA \right)}^{2}}\le 2A{{B}^{2}}$ $\Rightarrow BX+XA\le AB\sqrt{2}$ Tương tự ta có: $AY+YC\le AC\sqrt{2}$ Dấu “=” xảy ra khi AX = BX, AY = YC hay tam giác ABX vuông cân tại X, tam giác ACY vuông cân tại Y. Khi đó : Chu vi tứ giác $BXY{{C}_{max}}=(AB+AC)\sqrt{2}+BC$ Vậy chu vi tứ giác BXYC lớn nhất khi d đi qua A sao cho các tam giác ABX, ACY vuông cân. Bài 5. (0,5 điểm) 1) (Dành cho lớp 8B, 8C, 8D, 8E) Cho a, b, c là các số thực đôi một khác nhau thỏa mãn ${{a}^{3}}+{{b}^{3}}+{{c}^{3}}=3abc$. Tính giá trị của biểu thức $M=\left( a+b \right)\left( b+c \right)\left( c+a \right)+abc$ 2) (Dành riêng cho lớp 8A) Với a, b là các số thực thỏa mãn ${{a}^{3}}+{{b}^{3}}-3ab=-18$. Chứng minh rằng: $-9 < a+b < -1$ Giải $\Leftrightarrow ({{a}^{3}}+{{b}^{3}})+{{c}^{3}}-3abc=0$ $\Leftrightarrow ({{a}^{3}}+{{b}^{3}}+3{{a}^{2}}b+3a{{b}^{2}})-3ab\left( a+b \right)+{{c}^{3}}-3abc=0$ $\Leftrightarrow {{(a+b)}^{3}}+{{c}^{3}}-3ab\left( a+b \right)-3abc=0$ $\Leftrightarrow \left( a+b+c \right)\left[ {{\left( a+b \right)}^{2}}-(a+b).c+{{c}^{2}} \right]-3ab\left( a+b+c \right)=0$ $\Leftrightarrow \left( a+b+c \right)\left[ {{a}^{2}}+{{b}^{2}}+2ab-a.c-bc+{{c}^{2}}-3ab \right]=0$ $\Leftrightarrow \left( a+b+c \right)\left( {{a}^{2}}+{{b}^{2}}+{{c}^{2}}-ab-ac-bc \right)=0$ (*) Xét ${{a}^{2}}+{{b}^{2}}+{{c}^{2}}-ab-ac-bc$ $=\frac{1}{2}.(2{{a}^{2}}+2{{b}^{2}}+2{{c}^{2}}-2ab-2ac-2bc)$ $=\frac{1}{2}.\left[ ({{a}^{2}}-2ab+{{b}^{2}})+({{b}^{2}}-2bc+{{c}^{2}})+({{c}^{2}}-2ac+{{a}^{2}}) \right]$ $=\frac{1}{2}.\left[ {{(a-b)}^{2}}+{{(b-c)}^{2}}+{{(c-a)}^{2}} \right]$ khác 0 vì a,b,c đôi một khác nhau. Do đó từ (*) suy ra $a+b+c=0$ $\Rightarrow \left\{ \begin{align} & a+b=-c \\ & b+c=-a \\ & c+a=-b \\ \end{align} \right.$ $M=\left( a+b \right)\left( b+c \right)\left( c+a \right)+abc=(-c).(-a).(-b)+abc=-abc+abc=0$ Vậy M = 0 Theo câu a) ta có: ${{a}^{3}}+{{b}^{3}}+{{c}^{3}}-3abc=\frac{1}{2}.(a+b+c).\left[ {{(a-b)}^{2}}+{{(b-c)}^{2}}+{{(c-a)}^{2}} \right]$ Áp dụng : ${{a}^{3}}+{{b}^{3}}-3ab=-18$ $\Leftrightarrow {{a}^{3}}+{{b}^{3}}+1-3a.b.1=-17$ $\Leftrightarrow \frac{1}{2}(a+b+1)\left[ {{(a-b)}^{2}}+{{(a-1)}^{2}}+{{(b-1)}^{2}} \right]=-17$ $\Leftrightarrow \frac{1}{2}(a+b+1)$< 0 vì ${{(a-b)}^{2}}+{{(a-1)}^{2}}+{{(b-1)}^{2}}$ > 0 với mọi $a,b,c$ $\Leftrightarrow a+b+1<0$ $\Leftrightarrow a+b<-1$ (1) Lại có: ${{(a-b)}^{2}}+{{(a-1)}^{2}}+{{(b-1)}^{2}}$$\ge $${{(a-1)}^{2}}+{{(b-1)}^{2}}={{a}^{2}}+{{b}^{2}}-2(a+b)+2$ Mà ${{a}^{2}}+{{b}^{2}}\ge \frac{{{(a+b)}^{2}}}{4}$ nên ${{(a-b)}^{2}}+{{(a-1)}^{2}}+{{(b-1)}^{2}}$$\ge \frac{{{(a+b)}^{2}}}{4}-2(a+b)+2$ $>\frac{1}{4}-2.(-1)+2=\frac{17}{4}$ vì $a+b<-1$ Thay vào $\frac{1}{2}(a+b+1)\left[ {{(a-b)}^{2}}+{{(a-1)}^{2}}+{{(b-1)}^{2}} \right]=-17$ ta được $a+b+1=\frac{-34}{{{(a-b)}^{2}}+{{(a-1)}^{2}}+{{(b-1)}^{2}}}>\frac{-34}{\frac{17}{4}}$ $\Leftrightarrow $$a+b+1>-8$ $\Leftrightarrow $$a+b>-9$ (2) Từ (1) và (2) suy ra $-\,9 < a+b < -1$ (đpcm) Tác giả: Vinastudy Cộng đồng zalo giải đáo bài tập Các bạn học sinh tham gia nhóm zalo để trao đổi giải đáp bài tập nhé ******************************** Hỗ trợ học tập: _Kênh Youtube:http://bit.ly/vinastudyvn_tieuhoc _Facebook fanpage:https://www.facebook.com/767562413360963/ _Hội học sinh Vinastudy Online:https://www.facebook.com/groups/online.vinastudy.vn/
Con sinh năm 2009
https://zalo.me/g/cieyke829
Con sinh năm 2010
https://zalo.me/g/seyfiw173
Con sinh năm 2011
https://zalo.me/g/jldjoj592
Con sinh năm 2012
https://zalo.me/g/ormbwj717
Con sinh năm 2013
https://zalo.me/g/lxfwgf190
Con sinh năm 2014
https://zalo.me/g/bmlfsd967
Con sinh năm 2015
https://zalo.me/g/klszcb046
Khách hàng nhận xét
Đánh giá trung bình
4/5
(7 nhận xét)
1
29%
2
0%
3
0%
4
0%
5
71%
Chia sẻ nhận xét về sản phẩm
Gửi nhận xét của bạn
1. Đánh giá của bạn về sản phẩm này: (*)
2. Tên của bạn: (*)
3. Email liên hệ:
3. Viết nhận xét của bạn: (*)
* Những trường có dấu (*) là bắt buộc.
* Để nhận xét được duyệt, quý khách lưu ý tham khảo Tiêu chí duyệt nhận xét của Vinastudy
-
![]()
Trần Ngọc Lan Anh
That's very helpful
Các tin mới nhất
Ngày đăng: 2023/12/06
Ngày đăng: 2022/12/23
Ngày đăng: 2022/12/23
Ngày đăng: 2022/12/23
Ngày đăng: 2022/12/23
Ngày đăng: 2022/12/23
Ngày đăng: 2022/12/08
Ngày đăng: 2022/12/08
Ngày đăng: 2022/12/08
Ngày đăng: 2022/12/08

.png)
.png)
.png)
.png)
.png)
.png)
.png)
.png)
.png)
.png)



