BỘ 15 ĐỀ THI GIỮA HỌC KỲ I MÔN TOÁN LỚP 7

Ngày đăng: 10/10/2019

 Cộng đồng zalo giải đáo bài tập 

Các bạn học sinh tham gia nhóm zalo để trao đổi giải đáp bài tập nhé 

Con sinh năm 2009	https://zalo.me/g/cieyke829
Con sinh năm 2010	https://zalo.me/g/seyfiw173
Con sinh năm 2011	https://zalo.me/g/jldjoj592
Con sinh năm 2012	https://zalo.me/g/ormbwj717
Con sinh năm 2013	https://zalo.me/g/lxfwgf190
Con sinh năm 2014	https://zalo.me/g/bmlfsd967
Con sinh năm 2015	https://zalo.me/g/klszcb046

Hệ thống giáo dục vinastudy.vn xin được gửi đến các em học sinh bộ đề thi giữa học kỳ 1 môn Toán lớp 7. Kính mong quý phụ huynh, thầy cô và các em học sinh đón xem.

 

Đề số 1

TRƯỜNG THPT CHUYÊN HÀ NỘI – AMSTERDAM TỔ TOÁN - TIN

ĐỀ KIỂM TRA GIỮA HỌC KỲ I NĂM HỌC: 2018 – 2019 Môn: TOÁN LỚP 7 Thời gian làm bài: 45 phút

 

Bài 1. (4,0 điểm)

Tính hợp lí (nếu có thể) các biểu thức sau:

1. a) $A=-1\frac{1}{3}:{{\left( \frac{1}{3}-\frac{1}{2} \right)}^{2}}-{{\left( -0,25 \right)}^{2}}:{{\left( \frac{1}{4}-\frac{1}{2} \right)}^{3}}$
2. b) $B=\sqrt{\frac{25}{4}}-14\sqrt{1-\frac{48}{49}}+\frac{1}{8}\sqrt{{{\left( -4 \right)}^{2}}}-\left| -{{5}^{2}} \right|$

Bài 2. (3,0 điểm)

1. a) Tìm các giá trị của $x$ thỏa mãn $3x-\left| x-\frac{1}{2} \right|=3$
2. b) Tìm các giá trị $x,y,z$ thỏa mãn $7x=3y,\,\,5y=7z$ và $xy+xz-yz=4$
3. c) Cho ba số $a,b,c$ đôi một khác nhau và khác 0 thỏa mãn $\frac{1}{c}+\frac{1}{a-b}=\frac{1}{a}-\frac{1}{b-c}$.

Chứng minh rằng $b=a+c$

Bài 3. (3,0 điểm)

Cho tam giác $ABC$ có số đo $\widehat{BAC}={{90}^{0}}$. Kẻ đường cao $AH$ của $\Delta ABC$ và tia phân giác $AM$ của góc $BAH(M\in BC).$

1. a) Chứng minh: $\widehat{ABC}=\widehat{HAC}$
2. b) Cho $\widehat{MAC}={{70}^{0}}$. Tính số đo $\widehat{AMC}$

---------------------------Hết---------------------------

 

 

Đề số 2

TRƯỜNG THCS MINH KHAI

ĐỀ KIỂM TRA GIỮA HỌC KÌ I NĂM HỌC: 2018 – 2019 Môn: TOÁN LỚP 7 Thời gian làm bài: 90 phút

 A. Phần trắc nghiệm (2 điểm)

Câu 1. Kết quả của phép tính ${{\left( -\frac{1}{2} \right)}^{2}}:\frac{3}{4}$ là:

A. $-\frac{1}{3}$

B. $\frac{1}{3}$

C. $\frac{-3}{16}$

D. $\frac{3}{16}$

Câu 2. Giá trị của $x$ thỏa mãn ${{\left( 3x-2 \right)}^{2}}=16$ là:

A. $2$ và $\frac{-2}{3}$

B. $-2$ và $\frac{2}{3}$

C. $\frac{4}{3}$ và 0

D. $x\in \varnothing $

Câu 3. Cho hai đường thẳng $a$ và $b$ song song với nhau. Đường thẳng $c$ vuông góc với $b$ thì:

A. $c\bot a$

B. $c$ cắt $a$

C. $c//a$

D. $c$ trùng với $a$

Câu 4. Cho hình vẽ, $a//b$ nếu:

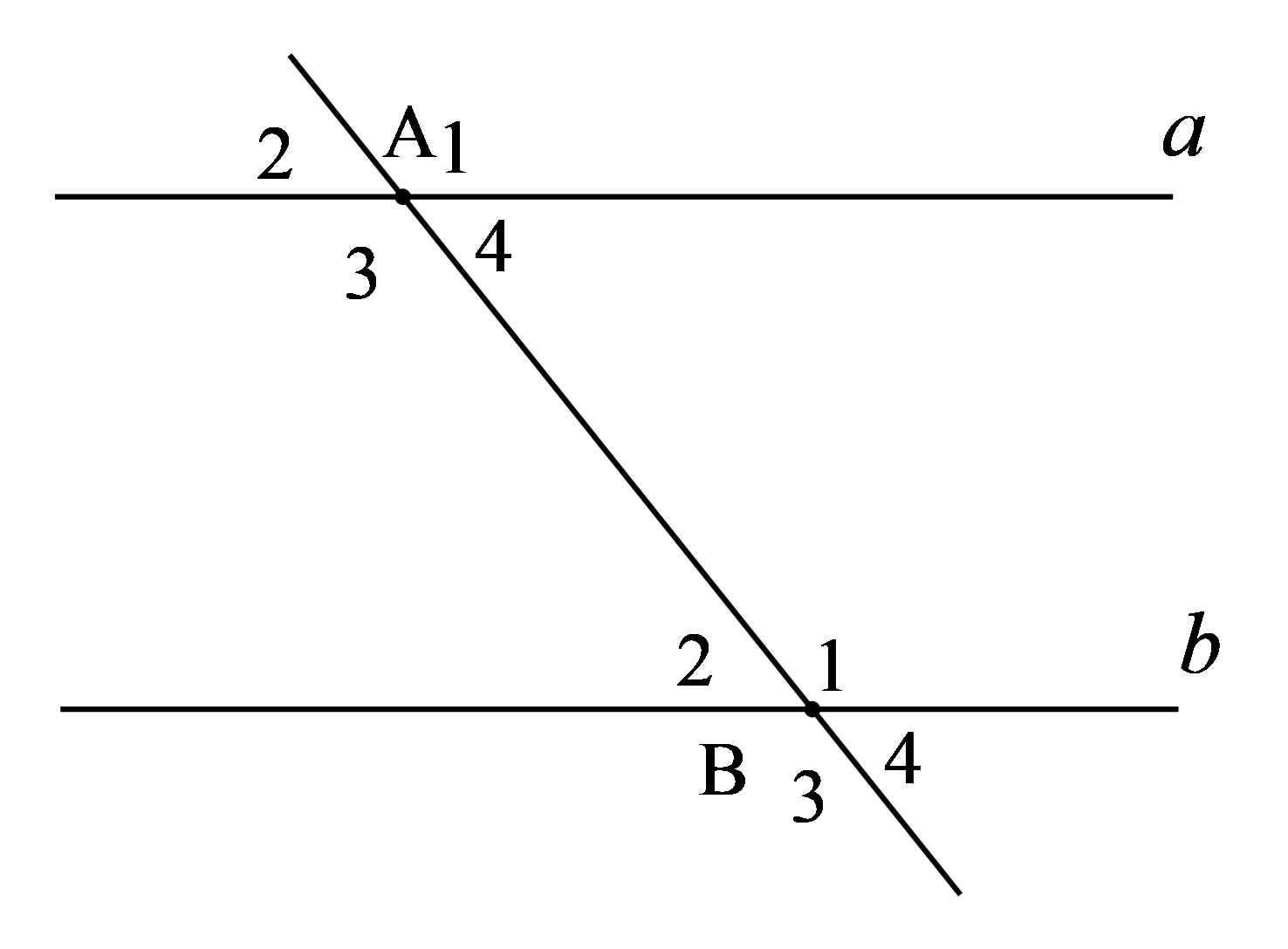
A. $\widehat{{{A}_{1}}}=\widehat{{{B}_{4}}}$

B. $\widehat{{{A}_{4}}}=\widehat{{{B}_{1}}}$

C. $\widehat{{{A}_{3}}}+\widehat{{{B}_{3}}}={{180}^{0}}$

D. $\widehat{{{A}_{4}}}=\widehat{{{B}_{2}}}$

B. Phần tự luận (8 điểm)

Bài 1. (1,5 điểm). Thực hiện phép tính

a) $\frac{5}{7}.\left( -\frac{3}{11} \right)+\frac{5}{7}.\left( -\frac{8}{11} \right)+2\frac{5}{7}$

b) $25.{{\left( -\frac{1}{5} \right)}^{3}}+\frac{1}{5}-2{{\left( -\frac{1}{2} \right)}^{2}}-\frac{1}{2}$

c) $\frac{{{5}^{102}}{{.9}^{1009}}}{{{3}^{2018}}{{.25}^{50}}}$

Bài 2. (1,5 điểm). Tìm $x$ biết:

a) $\frac{x}{4}=\frac{3}{10}$

b) $\left| x+\frac{1}{5} \right|-4=-2$

c) ${{\left( x+\frac{1}{2} \right)}^{2}}=\frac{1}{16}$

Bài 3. (2 điểm). Một khu đất hình chữ nhật có chu vi bằng 32m, tỉ số giữa chiều dài và chiều rộng là $\frac{5}{3}$. Tính diện tích của mảnh đất hình chữ nhật đó.

Bài 4. (2,5 điểm) Cho tam giác $ABC$ có $\widehat{B}={{65}^{0}},\,\,\widehat{C}={{65}^{0}}.$ Kẻ tia $Ax$ là tia đối của tia $AB.$ Vẽ tia $Ay$ song song với $BC$ với tia $Ay$ nằm giữa hai tia $Ax,\,\,AC$.

a) Tính $\widehat{BAC}$

b) Tính $\widehat{BAy}$

c) Chứng minh tia $Ay$ là tia phân giác của $\widehat{xAC}$

Bài 5 (0,5 điểm) Cho $a+c=2b$ và $2bd=c\left( b+d \right)$ (với $b,d$ khác 0). Chứng minh $\frac{a}{b}=\frac{c}{d}$.

------------------------------HẾT------------------------------

 

 

Đề số 3

PHÒNG GIÁO DỤC VÀ ĐÀO TẠO QUẬN HÀ ĐÔNG ĐỀ CHÍNH THỨC

ĐỀ KIỂM TRA KSCL GIỮA KÌ I Năm học 2017 – 2018 Môn: TOÁN 7 Thời gian làm bài: 60 phút (Không kể thời gian giao đề)

A. TRẮC NGHIỆM KHÁCH QUAN (1 điểm)

Chọn chữ cái đứng trước câu trả lời đúng (viết vào bài làm).

Câu 1. Phân số nào sau đây viết được dưới dạng số thập phân vô hạn tuần hoàn?

A. $\frac{3}{2}$

B. $\frac{1}{4}$

C. $\frac{1}{7}$

D. $\frac{3}{15}$

Câu 2. Cho $12:x=6:5$ giá trị $x$ bằng:

A. $\frac{3}{2}$

B. $9$

C. $7$

D. $5$

Câu 3. Nếu $\sqrt{x}=6$ thì $x$ có giá trị là:

A. $\pm 36$

B. $12$

C. $-36$

D. $36$

Câu 4. Cho hình vẽ và biết $AB\parallel CD$ thì:

A. $x=y$

B. $y=180{}^\circ +x$

C. $y=x-180{}^\circ $

D. $x+y=180{}^\circ $

B. TỰ LUẬN (9 điểm)

Bài 1. (3 điểm) Tính giá trị của các biểu thức một cách hợp lí

$A=\left( 4-\frac{1}{4}+\frac{2}{3} \right)+\left( 5+\frac{4}{3}-\frac{6}{5} \right)-\left( 6+\frac{7}{4}+\frac{4}{5} \right)$                        $B=\frac{{{(-1)}^{6}}{{.3}^{5}}{{.4}^{3}}}{{{9}^{2}}{{.2}^{5}}}$

Bài 2. (3 điểm) Tìm $x,y$ biết:

a) $\left| x+\frac{3}{4} \right|-\frac{1}{3}=0$

b) $\frac{1}{9}{{.3}^{4}}{{.3}^{x}}={{3}^{7}}$

c) $\frac{x}{6}=\frac{y}{5}$ và $x-y=-28$

Bài 3. (2 điểm) Cho hình vẽ:

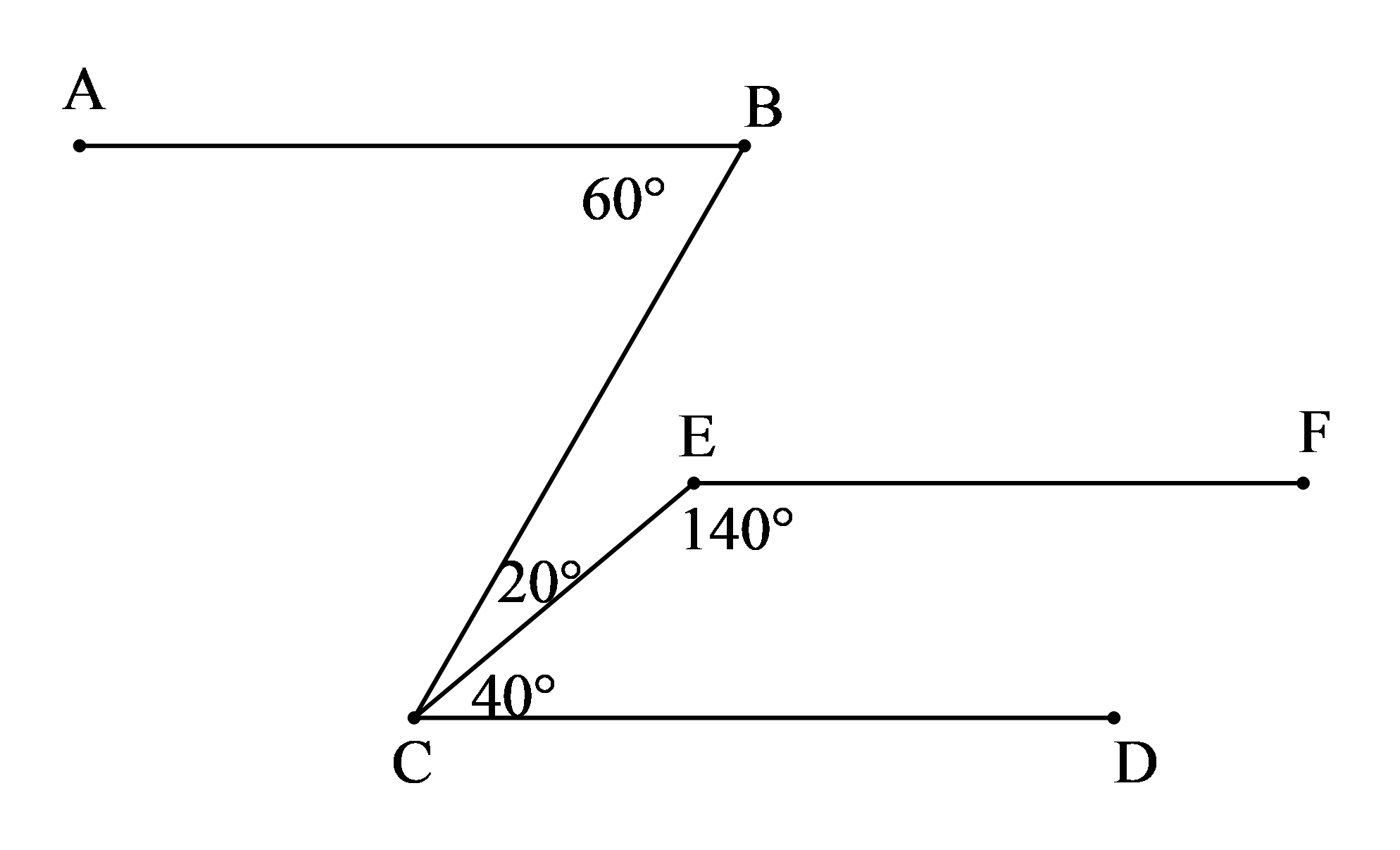
a) Hãy xét xem $AB$ có song song với $EF$ hay không?

b) Qua $E$ kẻ $Ex$ là tia phân giác của góc $CEF$, $Ex$ cắt $CD$ tại $M.$ Tính góc $EMC$.

Bài 4. (1 điểm) Chứng minh rằng nếu $\frac{{{a}_{1}}}{{{a}_{2}}}=\frac{{{a}_{2}}}{{{a}_{3}}}=\frac{{{a}_{3}}}{{{a}_{4}}}=...=\frac{{{a}_{2017}}}{{{a}_{2018}}}$ thì:

$\frac{{{a}_{1}}}{{{a}_{2018}}}={{\left( \frac{{{a}_{1}}+{{a}_{2}}+{{a}_{3}}+...+{{a}_{2017}}}{{{a}_{2}}+{{a}_{3}}+{{a}_{4+}}...+{{a}_{2018}}} \right)}^{2017}}$

 

------------------------------HẾT------------------------------

 

Đề số 4

TRƯỜNG THPT CHUYÊN HÀ NỘI – AMSTERDAM TỐ TOÁN - TIN

ĐỀ KIỂM TRA GIỮA HỌC KỲ I NĂM HỌC 2017 - 2018 Môn: Toán lớp 7 Thời gian làm bài: 45 phút

 

Bài 1: (2 điểm) Tính giá trị biểu thức sau:

A = ${{\left( -\frac{1}{2} \right)}^{7}}.{{\left( -\frac{1}{2} \right)}^{9}}:{{\left[ {{\left( -\frac{1}{2} \right)}^{3}} \right]}^{5}}-{{2}^{2}}.{{\left( -1\frac{1}{2} \right)}^{3}}-\frac{2}{3}.\sqrt{81}+{{\left( \sqrt{3} \right)}^{4}}$

Bài 2: (2 điểm)

     Cho biểu thức: M = $\frac{2x-1}{3x-1}$

     Hãy tìm các giá trị của $x$ sao cho:

1. a) M = 0
2. b) M < 0

Bài 3: (2 điểm)

     Sau khảo sát chất lượng giữa học kì, số học sinh của lớp 7A được xếp thành ba loại: giỏi, khá, trung bình. Số học sinh giỏi và khá theo thứ tự tỉ lệ với 2 và 3, số học sinh khá và trung bình theo thứ tự tỉ lệ với 5 và 6. Biết số học sinh khá ít hơn số học sinh trung bình là 3 em. Tính tổng số học sinh lớp 7A và số học sinh mỗi loại.

Bài 4: (4 điểm)

Cho tam giác ABC có $\widehat{A}={{60}^{0}}$, kẻ tia phân giác của góc B cắt AC ở D, tia phân giác góc C cắt AB ở E. Qua A kẻ đường thẳng song song với CE, đường thẳng này cắt đường thẳng BC tại F.

1. a) Chứng minh rằng: $\widehat{AFC}=\widehat{CAF}$ .
2. b) Chứng minh rằng: $\widehat{BDC}=\widehat{AEC}$.

 Chú ý: - Học sinh không được dùng tài liệu, máy tính cầm tay.

- Cán bộ coi thi không giải thích gì thêm.

------------------------------HẾT------------------------------

 

 

Đề số 5

PHÒNG GD&ĐT NAM TỪ LIÊM TRƯỜNG THCS MỸ ĐÌNH 1

ĐỀ KIỂM TRA KSCL GIỮA HỌC KỲ I NĂM HỌC 2018 – 2019 Môn kiểm tra: TOÁN 7 Thời gian làm gian: 90 phút

 

PHẦN 1. TRẮC NGHIỆM (1 điểm). Viết lại chữ cái đứng trước đáp án đúng trong các câu sau vào bài kiểm tra

Câu 1. Cho $12:x=3:5$ giá trị của $x$ bằng:

A. $10$

B. $5$

C. $20$

D. $4$

Câu 2. Kết quả của phép tính ${{\left( \frac{2}{3} \right)}^{3}}:{{\left( -\frac{2}{3} \right)}^{2}}$ là:

A. $1$

B. $-1$

C. $\frac{2}{3}$

D. $\frac{-2}{3}$

Câu 3. Nếu $m\bot b$ mà $m\bot c$ thì:

A. $b\bot c$

B. $m\parallel b$

C. $m\parallel c$

D. $b\parallel c$

Câu 4. Nếu một đường thẳng cắt hai đường thẳng song song thì:

A. Hai góc đồng vị phụ nhau C. Hai góc so le trong bù nhau

B. Hai góc trong cùng phía bù nhau D. Cả ba ý trên đều sai

Phần 2. TỰ LUẬN (9 điểm)

Bài 1 (2 điểm) Thực hiện phép tính (Tính nhanh nếu có thể)

a) $\frac{-5}{7}.\frac{31}{33}+\frac{-5}{7}.\frac{2}{33}+1\frac{5}{17}$

b) $\frac{4}{7}+\frac{3}{7}.\left( \frac{-2}{3} \right)$

c) $\frac{{{9}^{2}}{{.3}^{3}}}{{{3}^{7}}}.2018$

d) $3-{{\left( -\frac{7}{8} \right)}^{0}}+{{\left( \frac{1}{2} \right)}^{3}}.16$

Bài 2 (1,5 điểm) Tìm $x$, biết:

a) $3x+\frac{2}{3}=\frac{4}{5}$

b) $\left| \frac{1}{2}x+\frac{3}{5} \right|=\frac{1}{2}$

c) ${{2}^{x}}+{{2}^{x+4}}=544$

Bài 3 (2điểm) Bạn An có 35 viên bi bao gồm 3 màu xanh, đỏ, vàng. Số viên bi màu xanh và đỏ tỉ lệ với 2 và 3, số bi màu đỏ và vàng tỉ lệ với 4 và 5. Tính số viên bi mỗi loại.

Bài 4 (3 điểm)

Cho hình vẽ bên, biết rằng $DE\parallel Ax$, góc $BAx$ bằng $35{}^\circ $, góc $DBC$ bằng $55{}^\circ $, góc $BCy$ bằng $125{}^\circ .$

a) Tính góc $ABE.$

b) Chứng minh $Cy\parallel Ax$.

c) Chứng minh $AB\bot BC$.

Bài 5 (0,5 điểm) Cho $\frac{x}{z}=\frac{z}{y}.$ Chứng minh rằng $\frac{{{x}^{2}}+{{z}^{2}}}{{{y}^{2}}+{{z}^{2}}}=\frac{x}{y}$.

----------------------HẾT----------------------

 

Đề số 6

TRƯỜNG THCS NGUYỄN DU

ĐỀ KIỂM TRA GIỮA HỌC KÌ I Năm học 2017 – 2018 Môn: TOÁN 7 Thời gian: 90 phút (Không kể thời gian phát đề)

Bài 1 (2 điểm) Tính:

a) $\frac{-1}{4}+\frac{3}{4}$

b) ${{(0,125)}^{3}}{{.8}^{3}}$

c) $2\frac{1}{2}+\frac{4}{7}:\left( -\frac{8}{7} \right)$          

d) ${{\left( \frac{1}{3} \right)}^{2}}.3-\frac{2}{9}:\frac{2}{3}$

Bài 2 (2 điểm) Tìm $x$, biết:

a) $x-\frac{1}{2}=\frac{3}{2}$

b) $\frac{3}{2}x=\frac{-5}{6}$

c) $\left| x+\frac{3}{4} \right|-\frac{1}{2}=0$

d) ${{({{a}^{x}})}^{2}}={{a}^{18}},\,(a\ne 0;a\ne \pm 1)$

Bài 3 (2 điểm)

Số học sinh ba khối 6, 7, 8 tỉ lệ với các số 41; 29; 30. Biết rằng tổng số học sinh khối 6 và 7 là 140 học sinh. Tính số học sinh mỗi khối.

Bài 4 (3 điểm)

Cho hình vẽ bên, biết $\widehat{{{B}_{1}}}=75{}^\circ ,a\bot c,b\bot c$.

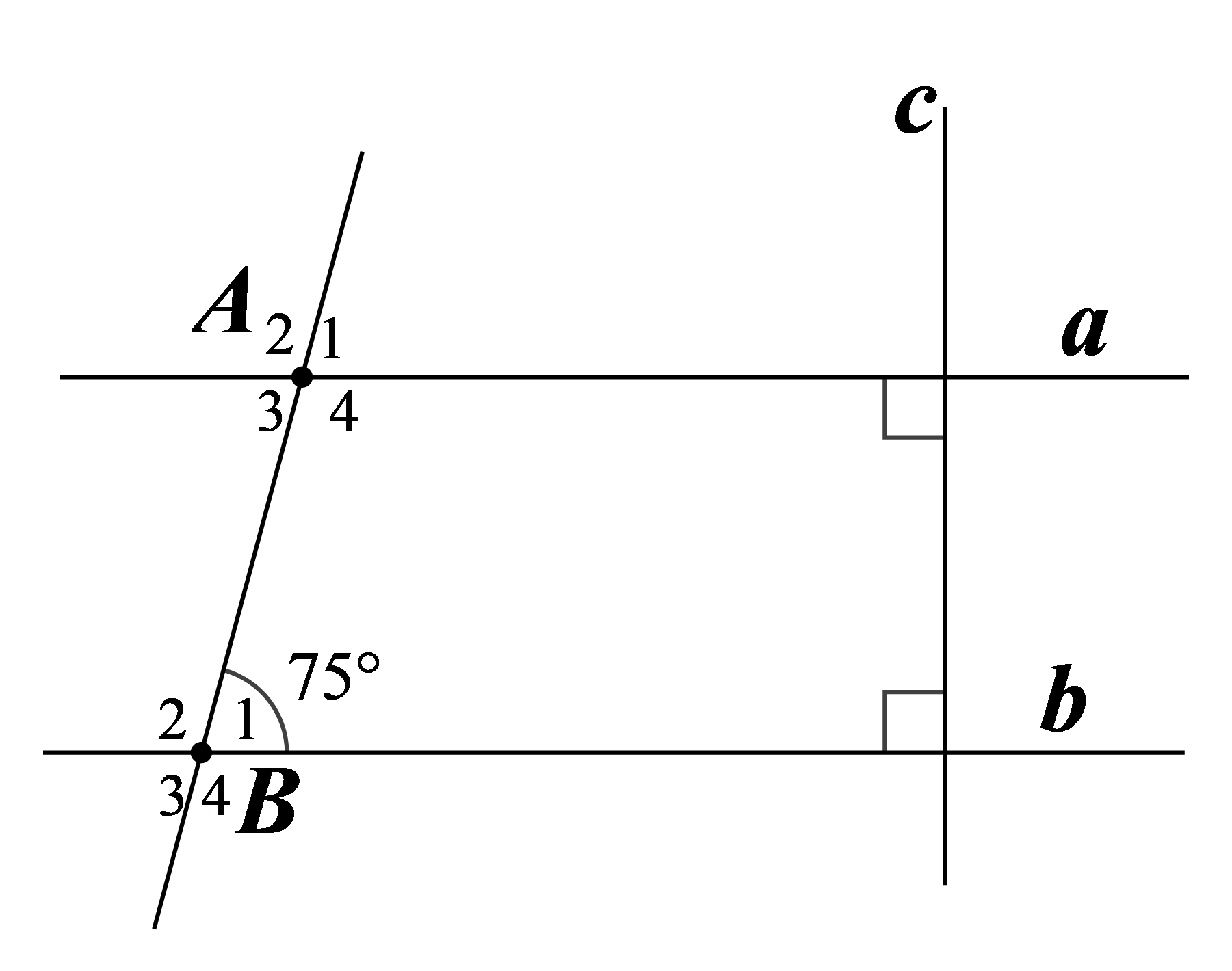
a) $a$ có song song với $b$ không ? Vì sao?

b) Tính $\widehat{{{A}_{1}}}.$

c) Tính $\widehat{{{A}_{4}}}.$

Bài 5 (1 điểm) Cho $a,b,c$ là các số khác $0$ sao cho:  $\frac{a+b-c}{c}=\frac{a-b+c}{b}=\frac{-a+b+c}{a}$

Tính giá trị biểu thức $M=\frac{(a+b)(b+c)(c+a)}{abc}$.

--------------------------HẾT-------------------------

Đề số 7

TRƯỜNG THCS TÔ HIỆU

ĐỀ THI GIỮA HỌC KÌ I NĂM HỌC 2016 – 2017 MÔN: TOÁN 7 Thời gian làm bài: 90 phút

 

PHẦN TRẮC NGHIỆM KHÁCH QUAN (2 điểm)

Hãy khoanh tròn vào chữ cái in hoa đứng trước đáp số đúng.

Câu 1. Cách viết nào sau đây là đúng:

A. $\left| -0,25 \right|=-0,25$ C. $-\left| -0,25 \right|=-(-0,25)$

B. $-\left| -0,25 \right|=-0,25$ D. $\left| -0,25 \right|=0,25$

Câu 2. Cho đường thẳng $c$ cắt hai đường thẳng $a$ và $b$ và trong các góc tạo thành có một góc so le trong bằng nhau thì:

A. $a\parallel b$

B. $a$ cắt $b$

C. $a\bot b$

D. $a$ trùng với $b$

Câu 3. Điểm thuộc đồ thị hàm số $y=-2x$ là:

A. $(1;-2)$

B. $\left( \frac{1}{2};-4 \right)$

C. $(0;2)$

D. $(-1;2)$

Câu 4. Tam giác $ABC$ vuông tại $A$ ta có:

A. $\widehat{B}+\widehat{C}>90{}^\circ $

B. $\widehat{B}+\widehat{C}<90{}^\circ $

C. $\widehat{B}+\widehat{C}=90{}^\circ $

D. $\widehat{B}+\widehat{C}=180{}^\circ $

PHẦN TỰ LUẬN (8,0 điểm)

Câu 1 (2 điểm)

a) Viết dạng tổng quát nhân hai lũy thừa có cùng cơ số.

b) Áp dụng tính ${{\left( \frac{1}{2} \right)}^{3}}.{{\left( \frac{1}{2} \right)}^{2}}$

Câu 2 (1,5 điểm) Tìm $x$, biết:

a) $2x+6=4$ b) $-\frac{2}{3}:x+\frac{5}{8}=-\frac{7}{12}$

Câu 3 (1 điểm) Một tam giác có chu vi bằng 36cm, ba cạnh của nó tỉ lệ thuận với $3;4;5.$ Tính độ dài ba cạnh của tam giác đó.

Câu 4 (3 điểm)

Cho tam giác $ABC$ vuông tại $A$, có $AB=AC.$ Gọi $K$ là trung điểm của cạnh $BC.$

a) Chứng minh $\Delta AKB=\Delta AKC$ và $AK\bot BC.$

b) Từ $C$ kẻ đường vuông góc với $BC,$ nó cắt $AB$ tại $E.$ Chứng minh $EC\parallel AK.$

Câu 5 (0,5 điểm)

Cho $\frac{1}{c}=\frac{1}{2}\left( \frac{1}{a}+\frac{1}{b} \right)$ (với $a,b,c\ne 0;\,b\ne c$). Chứng minh rằng $\frac{a}{b}=\frac{a-c}{c-b}$.

-------------------------HẾT-------------------------

 

Đề số 8

 

TRƯỜNG THCS ARCHIMEDES Đề số 1

ĐỀ KIỂM TRA THÁNG 9 Năm học: 2019 – 2020 MÔN TOÁN LỚP 7 Thời gian làm bài 90 phút

 

Học sinh làm bài và trình bày chi tiết, không sử dụng máy tính!

Câu 1. (2 điểm) Tính:

a) $1\frac{2}{5}-2\frac{3}{4}-\left( 1\frac{1}{4}-\frac{3}{5} \right)$

b) $\frac{1}{3}.\frac{-4}{5}.{{\left( -\frac{1}{2} \right)}^{2}}:\frac{1}{12}$

c) $\frac{3}{11}.\frac{-2}{5}-\frac{8}{11}.\frac{2}{5}$

d) $\left( 1+\frac{1}{3}-\frac{2}{5} \right)-\left( 2-\frac{2}{3}-\frac{3}{5} \right)+\left( 3-\frac{4}{3}-\frac{1}{5} \right)$

Câu 2. (2 điểm) Tìm số hữu tỉ $x$,  biết:

a) $x-\frac{1}{3}=\frac{6}{19}+\frac{-3}{9}$

b) $\frac{1}{x}.\frac{-2}{7}=\frac{3}{8}$

c) $\left| x-\frac{1}{4} \right|=\frac{2}{3}$

Câu 3. (2 điểm) Tìm số nguyên $a,b$ thỏa mãn:

a) $-\frac{19}{2}

b) $\frac{1}{3}<\frac{4}{b}<\frac{1}{2}$

Câu 4. (3,5 điểm) Học sinh vẽ lại hình vào bài!

Cho hình vẽ bên, biết $xy\parallel zt$ và $\widehat{zBv}=60{}^\circ $.

a) Kể tên các góc ở vị trí đối đỉnh, so le trong, đồng vị và trong cùng phía của góc $BAy$.

b) Tính số đo góc $BAy$.

c) Vẽ tia $Am$ là tia phân giác của góc $BAy$. Vẽ tia $Bn$ sao cho $Bz$ là là phân giác góc $\widehat{nBv}$. Chứng minh $Am\parallel Bn.$

Câu 5. (0,5 điểm) Học sinh chỉ chọn 1 trong 2 ý để làm!

Tính $A=\frac{1}{3}+\frac{13}{15}+\frac{33}{35}+\frac{61}{63}+\frac{97}{99}+\frac{141}{143}$

Tìm các số nguyên $x,y$ thỏa mãn: $2x+3y=19$ và $\frac{1}{3}<\frac{x}{y}<\frac{1}{2}$

Giám thị coi thi không giải thích gì thêm!

-------------------------HẾT-------------------------

 

Đề số 9

 

TRƯỜNG THCS ARCHIMEDES Đề số 2

ĐỀ KIỂM TRA THÁNG 9 Năm học: 2019 – 2020 MÔN TOÁN LỚP 7 Thời gian làm bài 90 phút

 

Học sinh làm bài và trình bày chi tiết, không sử dụng máy tính!

Câu 1. (2 điểm) Tính:

a) $1\frac{3}{4}+2\frac{2}{5}-\left( 1\frac{2}{5}-2\frac{1}{4} \right)$

b) $\frac{-1}{3}.\frac{5}{4}.{{\left( -\frac{1}{3} \right)}^{2}}:\frac{1}{18}$

c) $\frac{5}{13}.\frac{-2}{3}-\frac{8}{13}.\frac{2}{3}$

d) $\left( 1-\frac{2}{3}+\frac{3}{5} \right)-\left( 2+\frac{1}{3}-\frac{1}{5} \right)+\left( 3+\frac{1}{3}-\frac{4}{5} \right)$

Câu 2. (2 điểm) Tìm số hữu tỉ $x$,  biết:

a) $x-\frac{1}{2}=\frac{8}{17}+\frac{-4}{8}$

b) $\frac{1}{x}.\frac{-4}{5}=\frac{3}{7}$

c) $\left| x+\frac{1}{4} \right|=\frac{2}{3}$

Câu 3. (2 điểm) Tìm số nguyên $a,b$ thỏa mãn:

a) $\frac{20}{3}

b) $\frac{1}{-2}<\frac{4}{b}<\frac{1}{-3}$

Câu 4. (3,5 điểm) Học sinh vẽ lại hình vào bài!

Cho hình vẽ bên, biết $xy\parallel zt$ và $\widehat{NMy}=120{}^\circ $.

a) Kể tên các góc ở vị trí đối đỉnh, so le trong, đồng vị và trong cùng phía của góc $MNy$.

b) Tính số đo góc $zNv$.

c) Vẽ tia $Ma$ là tia phân giác của góc $NMy$. Vẽ tia $Nb$ sao cho $Nz$ là là phân giác góc $\widehat{bNv}$. Chứng minh $Ma\parallel Nb.$

Câu 5. (0,5 điểm) Học sinh chỉ chọn 1 trong 2 ý để làm!

Tính $A=\frac{1}{3}+\frac{13}{15}+\frac{33}{35}+\frac{61}{63}+\frac{97}{99}+\frac{141}{143}$

Tìm các số nguyên $x,y$ thỏa mãn: $2x+3y=19$ và $\frac{1}{3}<\frac{x}{y}<\frac{1}{2}$

Giám thị coi thi không giải thích gì thêm!

 -------------------------HẾT-------------------------

 

Đề số 10

TRƯỜNG THPT CHUYÊN HÀ NỘI – AMSTERDAM TỐ TOÁN - TIN

ĐỀ KIỂM TRA CHẤT LƯỢNG GIỮA HỌC KỲ I NĂM HỌC 2016 - 2017 Môn: Toán lớp 7 Thời gian làm bài: 90 phút

 

Bài 1: (4 điểm)

a) Tính: C = $\frac{{{\left( \frac{2}{5} \right)}^{7}}{{.5}^{7}}+{{\left( \frac{16}{3} \right)}^{3}}:{{\left( \frac{4}{9} \right)}^{3}}}{{{2}^{7}}{{.5}^{2}}+512}$

b) Tìm $x$ : $\left| \frac{1}{2}x-\frac{3}{4} \right|=1-x$

Bài 2: (2 điểm)

Ba lớp 7A, 7B, 7C có tất cả 153 học sinh. Số học sinh lớp 7C bằng $\frac{8}{9}$ số học sinh lớp 7B, số học sinh lớp 7A bằng $\frac{17}{16}$ số học sinh lớp 7C. Tính số học sinh của mỗi lớp.

Bài 3: (3 điểm)

Cho $\Delta ABC$ có $\widehat{A}={{50}^{0}}$. Lấy điểm $O$ ở trong tam giác $ABC$, nối $OB$, $OC$.

a) Tính góc $BOC$ biết góc $\widehat{ABO}=30{}^\circ ,\widehat{ACO}=40{}^\circ .$

b) Kẻ các tia $Bx$ và $Cy$ sao cho tia $BA$ là tia phân giác của $\widehat{OBx}$ , tia $CA$ là tia phân giác của $\widehat{OCy}$ . Kéo dài $CO$ cắt tia $Bx$ tại $D$, kéo dài $BO$ cắt tia $Cy$ tại $E$. Biết tỉ lệ số đo của 2 góc $BDC$và $BEC$ là 3: 2, hãy tính số đo mỗi góc.

Bài 4: (1 điểm)

Cho M = $\frac{3}{4}+\frac{{{3}^{2}}}{{{4}^{2}}}+\frac{{{3}^{3}}}{{{4}^{3}}}+...+\frac{{{3}^{2016}}}{{{4}^{2016}}}$ . Tìm phần nguyên của M.

---------------------------------HẾT ---------------------------------

 

Đề số 11

TRƯỜNG THCS NGUYỄN VĂN TRỖI Đề 1

ĐỀ THI GIỮA HỌC KÌ 1 Năm học 2017 – 2018 Thời gian: 90 phút

I) TRẮC NGHIỆM (4 điểm)

Khoanh tròn vào chữ cái ở đầu mỗi câu trả lời mà em cho là đúng nhất.

Cách viết nào biểu diễn số hữu tỉ:

A.  $3,(5)$

B. $\frac{-8}{15}$

C. $\frac{20}{0}$

D. $\sqrt{7}$

Làm tròn số 248,567 đến chữ số thập phân thứ nhất:

A. 250

B. 248

C. 248,6

D. 248,57

Biết $x:{{(-2)}^{5}}={{(-2)}^{3}}$. Kết quả $x$ bằng:

A. ${{(-2)}^{8}}$

B. 4

C. ${{(-2)}^{15}}$

D. ${{(-2)}^{7}}$

Cho $\left| x \right|-1=2$ thì:

A. $x=3$

B. $x=-3$

C. $x=\pm 2$

D. $x=\pm 3$

Cho tỉ lệ thức $\frac{x}{12}=\frac{-2}{3}$. Kết quả $x$ bằng:

A. -10

B. -9

C. -8

D. -7

Cho $\sqrt{m}=3$ thì ${{m}^{3}}$ bằng:

A. 3

B. 9

C. 729

D. 81

Phân số nào biểu diễn được dưới dạng số thập phân hữu hạn?

A. $\frac{5}{9}$

B. $\frac{7}{6}$

C. $\frac{6}{-14}$

D. $\frac{7}{50}$

Cho đẳng thức $8.6=4.12$ ta lập được tỉ lệ thức là:

A. $\frac{12}{4}=\frac{6}{8}$

B. $\frac{8}{4}=\frac{12}{6}$

C. $\frac{4}{12}=\frac{8}{6}$

D. $\frac{4}{8}=\frac{12}{6}$

II) TỰ LUẬN (6 điểm)

Bài 1. (1 điểm) Thực hiện phép tính:

a) $\frac{27}{23}+\frac{5}{21}-\frac{4}{23}+\frac{16}{21}+\frac{1}{2}$

b) $\frac{3}{2}-\frac{5}{6}:{{\left( \frac{1}{2} \right)}^{2}}+\sqrt{4}$

Bài 2. (1,5 điểm) Tìm $x$, biết:

a) $1\frac{2}{5}x+\frac{3}{7}=-\frac{4}{5}$

b) ${{\left( x+\frac{1}{3} \right)}^{3}}=\frac{-1}{8}$

c) $\left| x+\frac{2}{3} \right|+2=2\frac{1}{3}$

Bài 3. (1 điểm) Tìm $x,y$ biết $x:y=4:7$ và $x-y=24$.

Bài 4. (1,5 điểm) Hưởng ứng phong trào kế hoạch nhỏ của Liên Đội, ba chi đội 7A, 7B, 7C đã thu được tổng cộng 120 kg giấy vụn. Biết rằng số giấy vụn thu được của ba chi đội lần lượt tỉ lệ với 9; 7; 8. Hãy tính số giấy vụn mỗi chi đội thu được.

Câu 5. (1 điểm) Học sinh chọn một trong hai câu sau:

1. Cho $a,b,c$ là các số hữu tỉ khác không sao cho:

$\frac{a+b-c}{c}=\frac{a-b+c}{b}=\frac{-a+b+c}{a}$

2. Tính giá trị bằng số của biểu thức: $M=\frac{(a+b)(b+c)(c+a)}{abc}$

Chứng minh rằng: Với mọi số nguyên dương $n$ thì ${{3}^{n+2}}-{{2}^{n+2}}+{{3}^{n}}-{{2}^{n}}$ chia hết cho 10.

---------------------HẾT---------------------

 

 

 

Đề số 12

TRƯỜNG THCS NGUYỄN VĂN TRỖI Đề 2

ĐỀ THI GIỮA HỌC KÌ 1 Năm học 2017 – 2018 Thời gian: 90 phút

I) TRẮC NGHIỆM (4 điểm)

Khoanh tròn vào chữ cái ở đầu mỗi câu trả lời mà em cho là đúng nhất.

1. Nếu $\sqrt{x}=9$ thì $x=?$

A.  $x=3$

B. $x=-3$

C. $x=-81$

D. $x=81$

2. Kết quả nào sau đây là sai?

A. $-5\in \mathbb{Q}$

B. $\sqrt{2}\notin I$

C. $\mathbb{Q}\subset \mathbb{R}$

D. $7,5(6)\in \mathbb{Q}$

3. Biết $x:{{(-2)}^{5}}={{(-2)}^{3}}$. Kết quả $x$ bằng:

A. $4$

B. ${{(-2)}^{8}}$

C. ${{(-2)}^{15}}$

D. ${{(-2)}^{7}}$

4. Cho $\left| x \right|+3=2$ thì:

A. $x=1$

B. $x=-1$

C. $x=\pm 1$

D. $x\in \varnothing $

5. Cho tỉ lệ thức $\frac{x}{12}=\frac{-2}{3}$. Kết quả $x$ bằng:

A. -10

B. -9

C. -8

D. -7

6. Cho $\sqrt{m}=4$ thì ${{m}^{2}}$ bằng:

A. 2

B. 4

C. 256

D. 16

7. Phân số nào biểu diễn được dưới dạng số thập phân vô hạn không tuần hoàn?

A. $\frac{8}{16}$

B. $\frac{7}{6}$

C. $\frac{5}{10}$

D. $\frac{-1}{4}$

8. Biểu thức $\frac{{{2}^{3}}{{.2}^{5}}.2}{{{2}^{4}}}$ viết dưới dạng kuyx thừa của 2 là:

A. ${{2}^{5}}$

B. ${{2}^{6}}$

C. ${{2}^{3}}$

D. ${{2}^{4}}$

TỰ LUẬN (6 điểm)

Bài 1. (1 điểm) Thực hiện phép tính:

a) $\frac{1}{7}.\frac{-3}{8}+\frac{-13}{8}.\frac{1}{7}$

b) ${{(-3)}^{2}}.\frac{1}{3}-\sqrt{49}+{{(-5)}^{3}}:\sqrt{25}$

Bài 2. (1,5 điểm) Tìm $x$, biết:

a) $2x-\frac{5}{4}=\frac{20}{15}$

b) ${{\left( x-1 \right)}^{5}}=-32$

c) $\left| x+\frac{4}{5} \right|-\frac{1}{7}=0$

Bài 3. (1 điểm) Tìm $x,y$ biết $5x=8y$ và $y-x=-12$.

Bài 4. (1,5 điểm) Tính chu vi của một tam giác, biết tổng độ dài hai cạnh nhỏ hơn cạnh lớn 4cm và các cạnh của tam giác tỉ lệ với các số 3;4;5.

Câu 5. (1 điểm) Học sinh chọn một trong hai câu sau:

1. Cho $A=\frac{2}{{{3}^{2}}}+\frac{2}{{{5}^{2}}}+\frac{2}{{{7}^{2}}}+...+\frac{2}{{{2017}^{2}}}$. Chứng minh rằng $A<\frac{504}{1009}$.

2. Cho $a+c=2b$ và $2bd=c(b+d)\,\,(b\ne 0;d\ne 0)$. Chứng minh $\frac{a}{b}=\frac{c}{d}.$

---------------------HẾT---------------------

 

 

Đề số 13

TRƯỜNG THCS NGUYỄN VĂN TRỖI Đề 3

ĐỀ THI GIỮA HỌC KÌ 1 Năm học 2017 – 2018 Thời gian: 90 phút

I) TRẮC NGHIỆM (4 điểm)

Khoanh tròn vào chữ cái ở đầu mỗi câu trả lời mà em cho là đúng nhất.

1. Số $\sqrt{{{3}^{3}}+{{4}^{2}}}$ bằng:

A.  $3+4$

B. $5$

C. $\sqrt{7}$

D. $\sqrt{5}$

2. Kết quả của phép tính ${{7}^{6}}:{{7}^{5}}$ là:

A. ${{7}^{11}}$

B. $1$

C. $7$

D. ${{7}^{2}}$

3. Biết $\sqrt{3}=x$ thì ${{x}^{2}}$ bằng:

A. $3$

B. $9$

C. $27$

D. $81$

4. Cho $x=6,67254$. Khi làm tròn đến chữ số thập phân thứ ba thì số $x$ bằng:

A. $6,672$

B. $6,67$

C. $6,6735$

D. $6,673$

5. Cho tỉ lệ thức $\frac{2}{x}=\frac{4}{0,2}$. Kết quả $x$ bằng:

A. $x=0,1$

B. $x=2$

C. $x=0,2$

D. $x=0,4$

6. Trong các khẳng định sau, khẳng định nào sai?

A. $-3\in \mathbb{Q}$

B. $1,(23)\in I$

C. $1,245\in \mathbb{R}$

D. $5\in \mathbb{N}$

7. Phân số nào không biểu diễn được dưới dạng số thập phân hữu hạn?

A. $\frac{9}{24}$

B. $\frac{14}{12}$

C. $\frac{14}{-35}$

D. $\frac{-1}{4}$

8. Biểu thức $\frac{{{2}^{3}}{{.2}^{5}}.2}{{{2}^{4}}}$ viết dưới dạng lũy thừa của 2 là:

A. ${{2}^{5}}$

B. ${{2}^{6}}$

C. ${{2}^{3}}$

D. ${{2}^{4}}$

TỰ LUẬN (6 điểm)

Bài 1. (1 điểm) Thực hiện phép tính:

a) $\frac{2}{5}.\frac{-7}{8}-\frac{1}{8}.\frac{2}{5}$

b) ${{(-4)}^{2}}.\frac{1}{16}-\sqrt{36}+{{(-5)}^{3}}:\sqrt{625}$

Bài 2. (1,5 điểm) Tìm $x$, biết:

a) $\frac{3}{5}x-\frac{1}{2}=-\frac{1}{7}$

b) $\sqrt{2x-3}=5$ c) $\left| x-\frac{4}{5} \right|-\frac{3}{5}=0$

Bài 3. (1 điểm) Tìm $x,y$ biết $\frac{x}{y}=\frac{11}{7}$ và $x-y=12$.

Bài 4. (1,5 điểm) Số học sinh của ba lớp $7A,7B,7C$ của một trường tỉ lệ với $7;8;9$. Số học sinh lớp 7C nhiều hơn số học sinh lớp 7A là 10 em. Hỏi mỗi lớp có bao nhiêu học sinh?

Câu 5. (1 điểm) Học sinh chọn một trong hai câu sau:

1. Cho $x,y,z$ là ba số dương phân biệt. Hãy tính tỉ số $\frac{x}{y}$ biết $\frac{y}{-x+z}=\frac{x-y}{z}=\frac{-x}{y}$.

2. Cho $\frac{x}{2}=\frac{y}{5}=\frac{z}{7}$. Tính giá trị biểu thức $A=\frac{x-y+z}{x+2y-z}$.

 

-----------------------------HẾT-----------------------------

 

Đề số 14

PHÒNG GIÁO DỤC VÀ ĐÀO TẠO LỤC NGẠN

ĐỀ KIỂM TRA GIỮA HỌC KÌ I NĂM HỌC 2015 – 2016 MÔN TOÁN 7 Thời gian: 90 phút

Câu 1. (2 điểm) Thực hiện phép tính:

a) $\frac{2}{3}.\frac{5}{4}-\frac{3}{4}.\frac{2}{3}$

b) $2.{{\left( \frac{-3}{2} \right)}^{2}}-\frac{7}{2}$

Câu 2. (3 điểm)

Tìm $x$, biết:

a) $\left| x-1,4 \right|=1,6$ b) $\frac{3}{4}-x=\frac{4}{5}$

Tìm $x,y$ biết: $\frac{x}{3}=\frac{y}{5}$ và $y-x=24$.

Câu 3. (1,5 điểm)

Trong phong trào thi đua hái hoa điểm tốt, số hoa đạt được của ba bạn Linh, Nga, Hương lần lượt tỉ lệ với 3;2;4. Tính số hoa điểm tốt của mỗi bạn biết rằng tổng số hoa đạt được của ba bạn là 72 bông.

Câu 4. (3 điểm)

Cho hai đường thẳng $x{x}'$ và $y{y}'$ cắt nhau tại $O.$ Góc $xOy$ có số đo là $100{}^\circ .$ Tính số đo các góc tạo thành bởi hai đường thẳng $x{x}'$ và $y{y}'$.

Cho hình vẽ bên:

a) Vì sao $a\parallel b$?

b) Tính số đo của $\widehat{{{A}_{1}}};\widehat{{{A}_{4}}}$.

Câu 5. (0,5 điểm)

Cho ba số khác nhau từng đôi một và khác 0 thỏa mãn: $\frac{a}{b+c}=\frac{b}{a+c}=\frac{c}{a+b}$.

Chứng minh $\frac{b+c}{a}+\frac{a+c}{b}+\frac{a+b}{c}$ không phụ thuộc vào giá trị của $a,b,c.$

-----------------------HẾT-----------------------

 

 

Đề số 15

PHÒNG GD&ĐT QUẬN 3 TRƯỜN THCS LÊ QUÝ ĐÔN

ĐỀ KIỂM TRA GIỮA HỌC KÌ I Năm học 2015 – 2016 Môn học: TOÁN 7 Thời gian: 90 phút

Bài 1 (3 điểm) Thực hiện phép tính:

a) $\left( \frac{2}{5}-1\frac{1}{4} \right):2\frac{1}{10}$

b) $\left( -5-\frac{5}{9} \right):\left( -1\frac{3}{4} \right)+\left( 4+\frac{5}{9} \right):\left( -1\frac{3}{4} \right)$

c) $\frac{{{4}^{1007}}{{.9}^{1007}}}{{{3}^{3015}}{{.16}^{503}}}$

Bài 2 (2 điểm) Tìm $x$, biết:

a) $\frac{2}{7}x-1\frac{2}{5}=\frac{3}{5}$ b) $\left| x-\frac{2}{3} \right|-\frac{5}{4}=1$

Bài 3 (1 điểm) Tìm $x,y,z$ biết: $\frac{x}{2}=\frac{y}{3}=\frac{z}{-4}$ và $x-y-z=27$.

Bài 4 (2 điểm) Trong hình 1, biết:

$\widehat{{{D}_{1}}}=70{}^\circ ;\widehat{{{C}_{2}}}=110{}^\circ ;c\bot a.$

a) Chứng minh $a\parallel b$.

b) Chứng minh $c\bot b.$

Bài 5 (2 điểm) Trong hình 2, biết:

$DE\parallel Cy$, $\widehat{xAB}=40{}^\circ ;\widehat{ABE}=140{}^\circ ;\widehat{BCZ}=130{}^\circ $

a) Chứng minh $Ax\parallel DE.$

b) Chứng minh: $AB\bot BC.$

 

 

--------------------------HẾT--------------------------

 

 

 

 

Phụ huynh tham khảo khóa học tại website www.vinastudy.vn :

Vina 1 Toán nền tảng bám sát sách giáo khoa lớp 7: khoa-hoc-toan-co-ban-lop-7-nen-tang-va-mo-rong-c10844.html

Vina 2 Nâng cao Toán 7:  khoa-hoc-online-toan-nang-cao-lop-7-bi-quyet-hoc-gioi-toan-cua-thay-long-c10845.html

Vina 3 Bồi dưỡng học sinh giỏi Toán 7: vina-3-boi-duong-hsg-toan-7-dot-pha-nang-luc-toan-c20993.html

 

Tác giả: Vinastudy

 Cộng đồng zalo giải đáo bài tập 

Các bạn học sinh tham gia nhóm zalo để trao đổi giải đáp bài tập nhé 

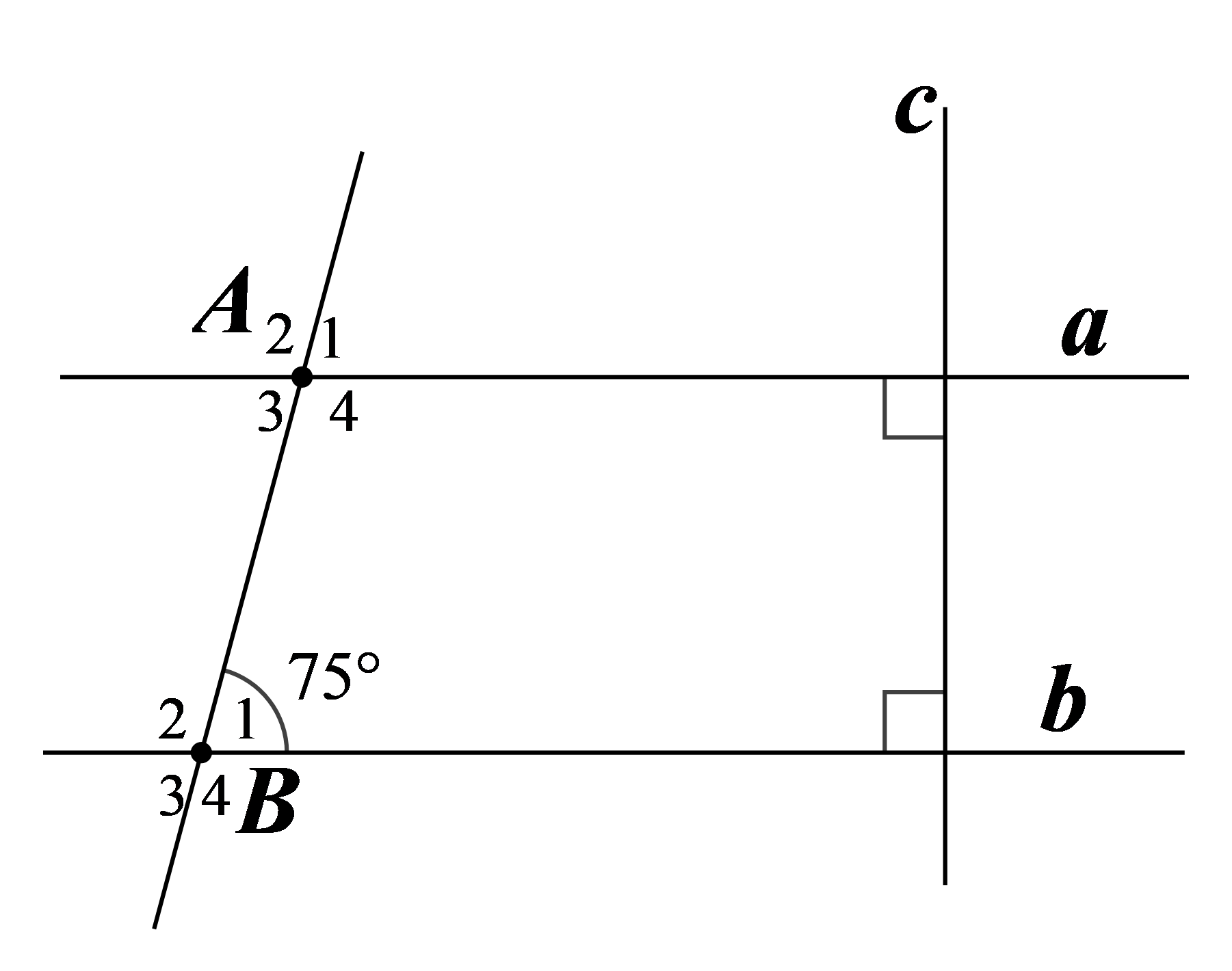
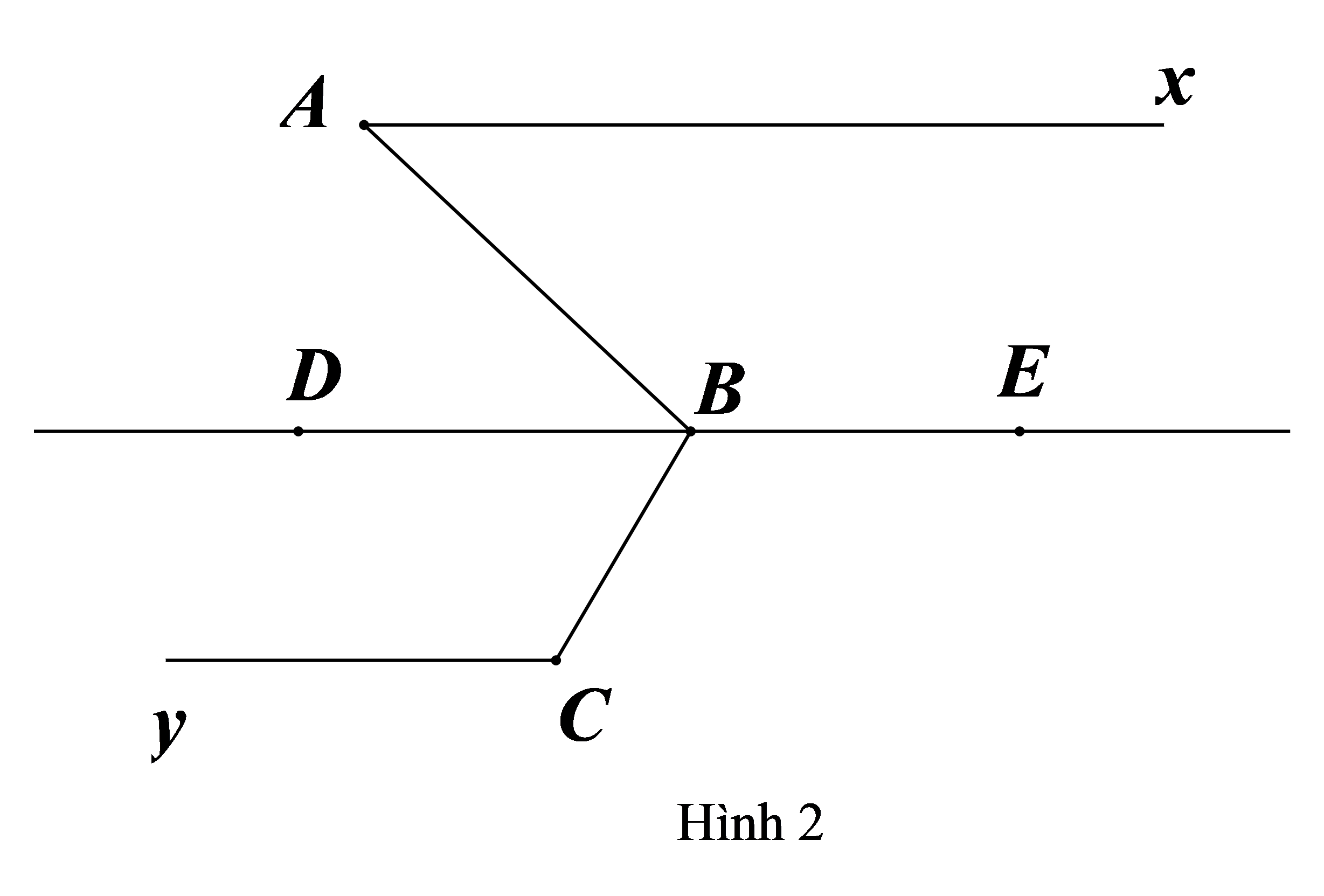
Con sinh năm 2009	https://zalo.me/g/cieyke829
Con sinh năm 2010	https://zalo.me/g/seyfiw173
Con sinh năm 2011	https://zalo.me/g/jldjoj592
Con sinh năm 2012	https://zalo.me/g/ormbwj717
Con sinh năm 2013	https://zalo.me/g/lxfwgf190
Con sinh năm 2014	https://zalo.me/g/bmlfsd967
Con sinh năm 2015	https://zalo.me/g/klszcb046

********************************

Hỗ trợ học tập:

_Kênh Youtube:http://bit.ly/vinastudyvn_tieuhoc

_Facebook fanpage:https://www.facebook.com/767562413360963/

_Hội học sinh Vinastudy Online:https://www.facebook.com/groups/online.vinastudy.vn/